Performance Analysis of Algorithms
By analysis of a program, we meant the amount of computer memory and time needed to run a program. In performance analysis we use analytical methods to determine the performance of the algorithm. In performance measurement we actually conduct experiments to measure the performance of algorithms. The performances of algorithms are measured based on concepts of Space Complexity and Time Complexity.
What is Space Complexity?
The “Space Complexity” of a program is the amount of memory it needs to run. Space complexity analysis is needed for following reasons.
1) If a program is to be run on a multi-user computer system, then we may need to specify the amount of memory to be allocated to the program.
2) For any computer system, we would like to know in advance whether or not, sufficient memory is available to run the program.
3) A problem might have several possible solutions with which different space requirements can be solved. e.g.:- Different compilers require different memory. Users with less memory will prefer compiler with less memory. So will users having extra memory because it leaves memory for other tasks.
4) We can use space complexity to estimate the size of largest problem that a program can solve.
What is Time Complexity?
The “Time Complexity” of a program is the amount of computer time it needs to run to completion. Time complexity analysis is needed for following reasons.
1) Some computer systems require the user to provide an upper limit on the amount of time the program will run. Once this upper limit is reached the program is aborted. Way out is to specify time limit of few thousand years. This solution could result in serious fiscal problems if the program runs into infinite loops. We would like to provide a time limit that is just slightly above the expected run time.
2) The program we are developing might need to provide a satisfactory real time response. A text editor that takes a minute to move the cursor one page down or up will not be accepted by users. Programs designed for interactive use must provide satisfactory real time response. From the time complexity of the program or program module we can decide whether or not the response time will be accepted.
3) If we have alternative ways to solve a program then the decision on which to use will be based primarily on the expected performance difference among these solutions.
Space Complexity
Components of Space complexity:-
1. Instruction Space :-
Instruction space is the space needed to store the compiled version of the program instructions.
2. Data Space :-
Data Space is the space needed to store all the constant and variable values. It has two components.
a) Space needed by constants and simple variables.
b) Space needed by component variables such as arrays. This includes space needed by structures and dynamically allocated memory.
3. Environment Stack Space :-
The environment stack is used to save information needed to resume execution of partially completed functions.
Instruction Space:-The amount of instruction space that is needed depends on factors such as:-
1) The compiler used to compile the program in to machine code.
2) The compiler options used at the time of compilation. Example: - The overlay option. This is the space assigned only to the program module that is currently executing. When a new module is invoked, it is read in from a disk or other device and the code for the new module overwrites the code of the old module. So program space corresponds to the size of the largest module.
3) The target computer configuration can also affect code size. If the computer has floating point hardware then floating point operators will translate into one m/c instruction per operation. If this hardware is not installed then code to simulate floating point computations will be generated.
Data Space:-For simple variables and constants, the space requirements are functions of the computer and compiler used as well as the size of the numbers involved. The reason is that we will normally be concerned with the number of bytes of memory required. Since the number of bits per byte varies from computer to computer, the numbers of bytes needed per variable also vary.
Environment Stack:-Each time a functions is invoked the following data are saved on the environment stack.
1) The return address
2) The values of all local variables and value formal parameters in the function being invoked.
3) The binding of all reference and constant reference parameters.
Summarizing Space Complexity:-The space needed by program depends on several factors. Some factors are not known at the time the program is written. So until these factors have been determined we cannot make an accurate analysis.
We can determine the contribution of those components that depend on characteristics of the program instance to be solved. The characters typically include factors that determine the size of the problem instance.
eg:- sort n elements :- space required is a function of n
:- add 2 n*n matrices :- we use n instance characteristics
The size of the instruction space is relatively insensitive to the particular problem instance being solved. The contribution of the constants and simple variables to the data structure is also independent of the characteristics of the problem instance to be solved except when the magnitude of the numbers involved becomes too large for the chosen data type in which case we will change the data type or rewrite the program using multi precision arithmetic.
The environment space is generally independent of the instance characteristics unless recursive functions are in use. When recursive functions are used the instance characteristics will generally affect the amount of space needed for the environment stack. The amount of stack space needed by the recursive functions is called the recursion stack space.
Analysis of Space Complexity Problems:-
We can divide the space complexity problem in two parts
a) A fixed part that is independent of the instance characteristics. This part typically includes the instruction space, space of simple variables and space for constants.
b) A variable part that consists of the space needed by component variables whose size depends on the particular problem instance being solved in dynamically allocated space and the recursion stack space.
The space requirement for any program P may be given as
S(P) = C + Sp
where c is a constant that denotes the fixed part of the space requirements and Sp denotes the variable component. An accurate analysis should also include the space needed by temporary variables during compilation. This space is compiler dependent and independent of instance characteristics except in recursive functions.
When analyzing the space complexity of a program we will need to concentrate solely on estimating Sp.
Example:- Sequential Search.
The following code examines a array “a” of “n” elements from left to right to see if one of these elements equals x. If an element equals to x is found, the function returns the position of the first occurrence of x else it returns -1.
templateint SequentialSearch( T a[], const T&x, int n)
{
int i;
for(i=0;i<n && a[i] != x; i++);
if(i==n) return -1;
return i;
}
We wish to find space complexity of this function in terms of the instance characteristics n.
Let us assume that T is int.
We need 2 bytes for each of the pointer to the array “a” and the actual parameter corresponding to x; 2 bytes for the formal value parameter n; 2 bytes for the local variable i and 2 bytes for each of the integer constants 0 and -1. The total space needed is 12 bytes. Since this space is independent of n, S(n)=0.
Note that array “a” must be large enough to hold n elements being searched. The space needed by this array is, however, allocated in the function where the actual parameter corresponding to a is declared.
Time Complexity
Components of Time Complexity
Time complexity of a program depends on all the factors that the space complexity depends on. A program will run faster on a computer capable of executing 109 instructions per second than on one that can execute 106 instructions per second.
The time T(P) taken by a program P is the sum of the compile time and the run time. The compile time does not depend on the instance characteristics. The runtime is denotes by Tp.
Because many of factors on which Tp depends on are not known when program is conceived, it is only possible to estimate Tp based on number of additions, subtractions, multiplications, divisions, compare, loading, storing and so on.
Letting n denote the instance characteristics, we might express Tp as
Tp(n) = caADD(n)+csSUB(n)+cmMUL(n)+cdDIV(n)+…
where ca, cs, cm and cd denote the time needed for addition, subtractions, multiplication and division and ADD, SUB, MUL and DIV are functions whose value is the number of additions, subtractions, multiplications and divisions performed when the code is used on an instance with “n” characteristics.
Further, time needed for each arithmetic operation depends on datatypes involved. This makes obtaining exact formulae difficult as we need to separate operation counts by data types.
Two more manageable methods are
1) Identify one or more key operations and determine number of times theses are performed.
2) determine the total number of steps executed by the program.
Operation Counts:-One way to estimate the time complexity of a program or functions is to select one or more operations such as add, multiply and compare to determine how many of each is done. The success of this method depends on ability to identify the operations that contribute most to the time complexity.
Example:- Selection Sort
One strategy to sort an array is to determine the largest element and move it so a[n-1], then determine the largest of the remaining n-1 elements and move it to a[n-2] and so on. For the following program we try to estimate the operation count by counting the number of element comparisons made.
template <classT> void SelectionSort (T a[],int n)
{
for (int size =n; size>1; size--)
{
int pos=0;
for(int i =1; i<n; i++)
if(a[pos] <a[i])
pos=i;
Swap(a[j], a[size-1]);
}
}
When each "i" loop is run, n-1 comparisons are made.
So the total number of comparisons is 1+2+3+...+n-1 = (n-1)n/2.
The number of element moves is 3(n-1), i.e. the Swap function.
So the time complexity of selection sort is (n-1)n/2
Step Counts:-The operation counts method omits accounting for the time spent on all but the chosen operations. In the step count method we attempt to account for the time spent in all parts of function or program. The step count is a function of the instance characteristics. Although any specific instance may have several characteristics (number of inputs, number of outputs, magnitude of input and outputs) the number of steps is computed as a function of some subset of these.
We choose the characteristics that are of interest to us. For example, we might wish to know how the computing time increases as number of input increasing. In this case number of steps will be computed as a function of number of inputs.
Thus before the step count of a program can be determined we need to know exactly which characteristics of the problem instance to be used. These characteristics define not only the variables in the expression for the step count but also how much computing can be counted as a single step. After an instance characteristics have been selected, we can define a step.
A step is any computation unit that is independent of the selected characteristics.
Definition:- A program step is loosely defined to be a syntactically or semantically meaningful segment of a program for which the execution time is independent of the instance characteristics.
We can determine number of steps that a program or function takes to complete a task by creating a global variable count with initial value zero. We introduce into program statements to increment count by the appropriate amount. Therefore each time statement in original program or function is executed, count id incremented by the step count of that statement. The value of count when the program or function terminates is the number of steps taken.
Example:- Sequential Search
We determine the Best case and worst case analysis of this algorithm.
The best case is when first item is the required item.
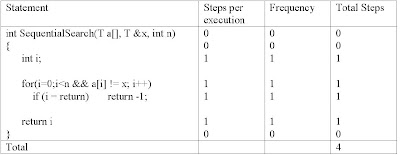
The worst case is when the search item is not found in the array.

For the average count analysis for a sequential search, assume that the n values in "a" are distinct and that in a successful search, x has equal probability of being any one of these values. Under these assumptions, the average step count for a successful search is the sum of the step counts for the n possible sucessful searches divided by n. To obtain this average, we first obtain step count for the cas x = a[j] where j is in range [0,n-1]


In next blog, I may discuss Asymptotic Notations (i.e. as much as I have understood).
For best understanding, read the book which I have mentioned in the beginning of the blog.
For reference you may visit following sites.
Analysis of Algorithms
http://www.cs.sunysb.edu/~algorith/lectures-good/
Programming Ring - New Post
Programming Ring - Old Post